11598. Запросы компании I

В компании n сотрудников, которые образуют древовидную иерархию, в которой у каждого сотрудника есть начальник, кроме генерального директора.

Ваша задача – обработать q запросов вида: кто является начальником сотрудника x на k уровнях выше в иерархии?

Вход. В первой строке записаны два целых числа n и q – количество сотрудников и запросов. Сотрудникам присвоены номера 1, 2, ..., n, а сотрудник 1 является генеральным директором.

В следующей строке записано n – 1 целых чисел e₂, e₃, ..., e_n: для каждого сотрудника 2, 3, ..., n указан его начальник.

Следующие q строк описывают запросы. Каждая строка содержит два целых числа x и k: кто является начальником сотрудника x на k-ом уровне выше?

Выход. Выведите ответ на каждый запрос. Если требуемого начальника не существует, то выведите -1.

Пример входа	Пример выхода
5 3 1 1 3 3 4 1 4 2 4 3	3 1 -1

РЕШЕНИЕ

двоичный подъем

Анализ алгоритма

Решим задачу методом двоичного подъема. Для каждой вершины i найдем вершину, которая находится на 2^j уровней выше. Запомним это значение в up[i][j].

Для нахождения начальника сотрудника x на k-ом уровне выше следует найти бинарное представление числа k. И совершить подьемы начиная с x на все степени двойки, которые входят в разложение числа k. Например, если k = 13 = 1101₂, то следует выполнить следующие операции:

· x = up[x][3] (поднимаемся на 8 шагов выше);

· x = up[x][2] (поднимаемся на 4 шага выше);

· x = up[x][0] (поднимаемся на 1 шаг выше);

Пример

Граф, представленный в примере, имеет вид:

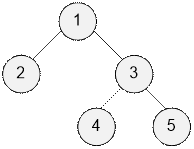
Например,

· up[4][0] = up[5][0] = 3;

· up[4][1] = up[5][1] = 1;

· up[2][0] = up[3][0] = 1.

Реализация алгоритма

Объявим массив up. Значение up[i][j] хранит начальника сотрудника i на 2^j уровней выше.

#define maxN 200001

#define logK 20

int up[maxN][logK];

Читаем входные данные. Для каждого сотрудника i читаем его непосредственного начальника up[i][0].

scanf("%d %d", &n, &q);

for (i = 2; i <= n; i++)

scanf("%d", &up[i][0]);

Методом двоичного подъема для каждого сотрудника i находим его начальника на уровне 2^j выше. Если такого начальника не существует, то up[i][j] = 0.

for (j = 1; j < logK; j++)

for (i = 1; i <= n; i++)

up[i][j] = up[up[i][j - 1]][j - 1];

Обрабатываем t запросов.

for (t = 0; t < q; t++)

{

scanf("%d %d", &x, &k);

При помощи бинарного подъема находим ответ на запрос.

for (i = 0; i < logK; i++)

if (k & (1 << i))

x = up[x][i];

Выводим ответ на запрос.

printf("%d\n", x ? x : -1);

}